About me
Thibault Cimic
2024-09-11 mer. 00:00
How to Use
- Press 'o' for navigation map and 'o' again to quit navigation map
- Press arrows keys to navigate
- Press space to follow the indented way
Introduction and contact info
Studies (2014-2018)
Master (2017-2018)
From LJLL at Sorbonne Université, specialisation in modelling focused on :
- Functional analysis :
- Sobolev/ Hilbert analysis
- PDEs modelisation :
- Finite differences/volumes/elements methods
- Discontinuous Galerkin methods
- Optimal control
- Shape optimization
Before that (2014-2017)
- First year of master :
- Large linear systems in C++
- Finite element method in python
- PDE analysis
- Statistics
- Licence :
- ODE in python
- Graph theory
- Topology theory
- Group theory
INRIA, Alpines (2018-2021)
Enlarged Conjugate Gradient (ECG)
Resume :
ECG(k) is a method for solving (SPD) linear systems as if one have deflated the smallest eigenvalue (without constructing any preconditioner).
- Build \( (K_k(A,b) \subset) EK_k(A,b)\) with :
\begin{equation} T_m : \mathbb{R}^n \rightarrow \mathbb{R}^{n \times m},\\
\forall x\in \mathbb{R}^n, T_m(x) \mathbb{1}_m = x
\end{equation}
- Build \( x_k \) with a ~CG on this \(EK_k(A,b)\)
- Converges as (p.44) :
\begin{equation}
\|x_l - x_*\|_A \leq c \left(\frac{\sqrt{\lambda_{max}} - \sqrt{\lambda_k}}{\sqrt{\lambda_{max}} + \sqrt{\lambda_k}}\right)^{l}
\end{equation}
Map-Making problem in CMB data analysis
- Resume :
Astrophysic :
One wants to build a high resolution map of the sky of properties (temperature, polarization) of the first lights in the universe (some 13.5 billions years ago).
Maths :
Build a fully algebraic 2-lvl preconditioner for a specific form of linear systems to bound the spectrum and reduce iterations.
Ones want to solve \( A x = b \) with :
\begin{equation}
A := P^T N P = \left( \sum_{i=1}^B P_{i}^T N_i P_i \right), b := P^T N d
\end{equation}
- Build \(Z_i = Span\left((v_{i,l})_{l=1...k}|\lambda_{i,k} \leq \frac{1}{\tau}\right)\) where :
\begin{equation}
N_i v_{i,l} = \lambda_{i,l} D_i v_{i,l}
\end{equation}
- Deflate \(Z = \underset{i=1}{\overset{B}{\oplus}} P_i^T M_i Z_i =: Span(Z_0) \) with :
\begin{equation}
M^{-1} := Z_0 \left( Z_0^T A Z_0 \right)^{-1} Z_0^T
\end{equation}
- End up with :
\begin{equation}
\Lambda \left( M^{-1}A \right) \subset \left[C_l(\tau), C_u \right]
\end{equation}
CEA, LGL (2023-2024)
Distribution of Ondo
- Ondo : C++ FE solver with high order, spectral polynomials
- Macro-mesh with Macro-Elements (ME)
- Micro-mesh inside each ME simulating one physic
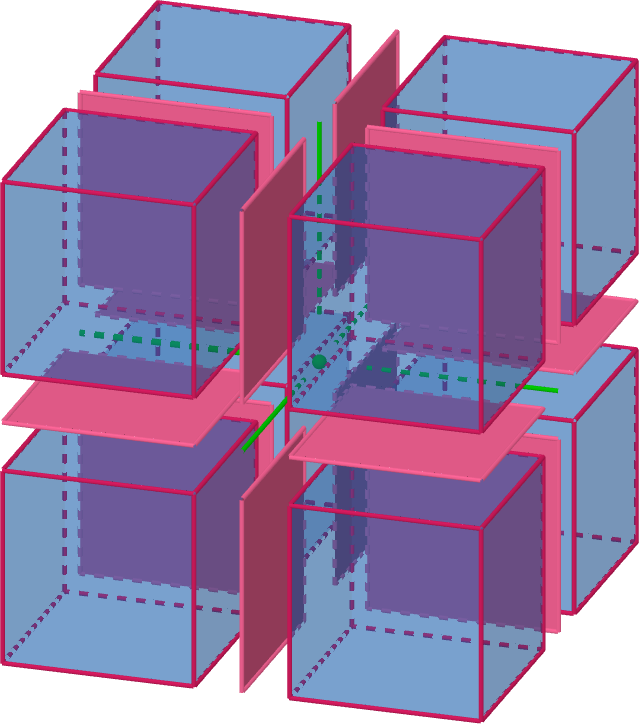
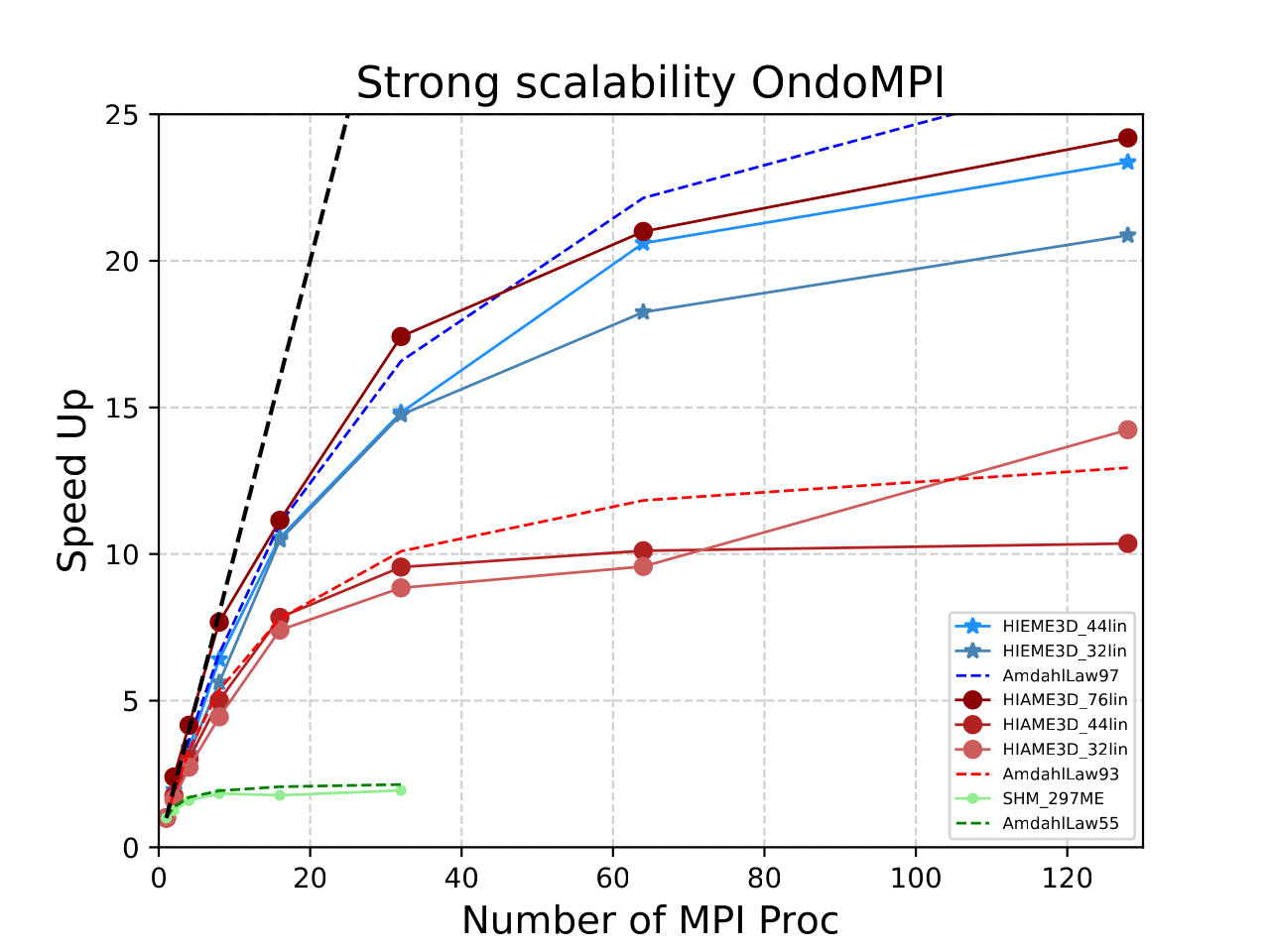
- OndoMPI :
- Design the distribution from scratch
- Build the necessary structures and modify existing ones
- Redesign construction algorithms and iterations
- Goals :
- Distribute the memory load
- Scale to a few hundreds procs
- Start the load balancing with Metis
- Constraints :
- Use blocking communication
- Have no collectives communications

Personal project
- Lina : Linear Algebra package in C++.
- MPIP++ : MPIP++ is a C++ API for MPI.
- BinaryContainers : BinaryContainers is a library to store C++ structures as contiguous blocks of memory.
Skill set resume
- Master :
- Solving large linear systems in C++
- Helmholtz with finite element in Python
- Navier-Stokes with finite element in C++
- INRIA :
- Solving distributed linear systems in C/MPI
- Solving large eigenvalue problems in C
- Build fully algebraic preconditioner in C/MPI
- CEA :
- Distribute a commercial finite element solver in C++/MPI
- C++ : 2.5 years
- 1.5 years in CIVA commercial software
- 1 years in master
- MPI : 3.5 years
- 1.5 years in CIVA commercial software
- 2 years at INRIA on the B3DCMB project
- C : 2 years
- 2 years at INRIA on the B3DCMB project
- Python : 1 year
- 1 year at INRIA
- Git : 4.5 years
- 3 years INRIA
- 1.5 years at CEA